Herkese merhaba,

Bu yazımda ML tahmin modellerinde linear regression analizinden bahsedeceğim. Numerik verisetlerinde tahminleme genelde lineer regresyon ile yapılır. Bu algoritma, bir niteliğin verilen değerleri üzerinden Least Squares Metodunu kullanarak başka niteliğin değerlerini tahmin etmeye çalışır. Lise matematiğinden bildiğimiz y= mx+ c doğru denklemi aslında veri setlerini ifade eden doğrusal regresyon fonksiyonunun ta kendisidir. Doğrunun eğimi de bize tahmini verir.

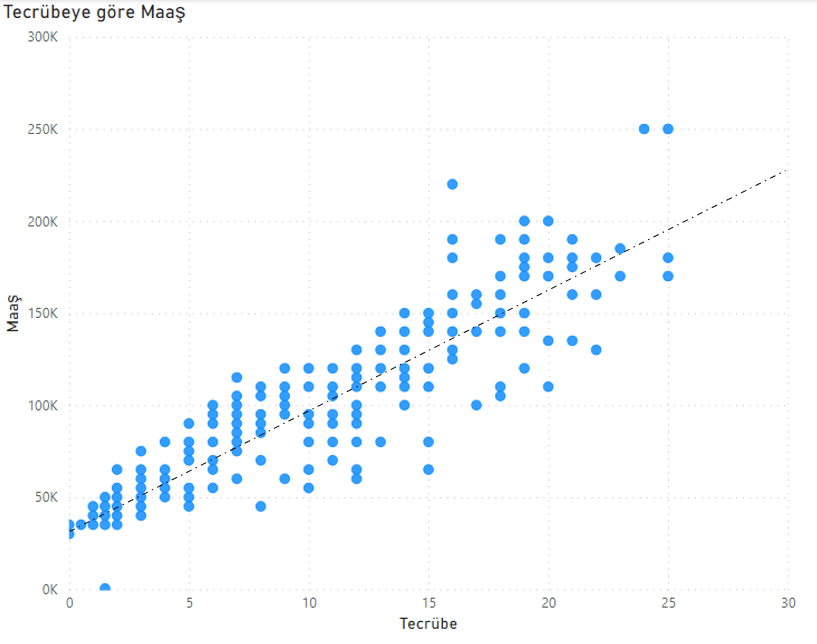
Bir örnek üzerinden gidelim ve tecrübe ile maaş grafiğinin dağılımına bakalım. x=0 durumuna karşılık gelen y değeri ve y=0’a karşılık gelen x değerleri üzerinden bu dağılımı en iyi ifade eden lineer regresyon fonksiyonunu tanımladığımızda bu doğrunun eğimi bize istediğimiz x değerine (yıl) karşılık gelen tahmini maaş (y) değerini verecektir. m ve c ne kadar iyi bilinirse verisetiyle o kadar uyumlu doğru denklemi elde edilmiş olur ve o kadar doğru tahmin elde edilir.

Burda veri fonksiyonunun hatasını azaltmak için Sum of Squares of Error (SSE) yada hataların kareleri toplamı kullanılır. Peki SSE nasıl hesaplanır?

• Fonksiyon veri setine uygulanır ve herbir veri için hedef niteliğin (yukarıdaki örnekte maaş) için tahminde bulunulur.
• Fonksiyonun hedef nitelik değeri ile gerçek nitelik değerleri arasındaki fark hesaplanır.
• Fonksiyonun herbir datadaki hatasının karesi alınır ( kare alınmasının nedeni hedef değer gerçek değerden küçük çıktığında sonuç negatif olur ve toplamda birbirini nötürleyebilir) ve toplanır.

Özetle Least Squares (en küçük kareler) metodu kullanılarak bulunan doğrusal regresyon fonksiyonu, ML modellerde ağırlıklandırılmış bir ortalama veriyor.

Burda maaş tahmininde tek bir parametreyi yani tecrübeyi ele aldık ama bu birden fazla parametreye bağlı bir fonksiyon da olabilirdi. Bu durumda lineer regresyon fonksiyonu aşağıdaki şekilde olur.

Yukarıdaki gibi çok girdili bir lineer regresyon fonksiyonu (multiple input linear regression) neural network (sinir ağı)’ün temelini oluşturur. Neural netwrok için bir sonraki yazıya bakabilirsiniz.